Рассмотрим случайную переменную X, принимающую одно из восьми возможных значений (х 1 ,x 2 , … , х 8) со следующими вероятностями:
P 1 = 0,512, Р 5 = 0,032,
Р 2 = 0,128, Р 6 = 0,032,
Р 3 = 0,128, Р 7 = 0,032,
Р 4 = 0,128, Р 8 = 0,008.
Здесь P i представляет собой вероятность выпадения результата х i . Предположим, что сообщение состоит из реализаций случайной переменной X, и мы хотели бы закодировать сообщение в двоичном виде. Один очевидный вариант решения заключается в том, чтобы использовать 3-битовый код фиксированной длины, в котором каждое из восьми возможных значений случайной переменной X кодируется одним 3-битовым числом. Лучшая стратегия заключается в использовании кода переменной длины, в котором более длинные кодовые слова назначаются менее вероятным значениям X, а более вероятные значения X кодируются короткими кодовыми словами. Такой технический прием применяется в азбуке Морзе и коде Хаффмана. Предположим, что сообщения должны передаваться при помощи алфавита из N символов. Каждый символ должен уникальным образом кодироваться двоичной последовательностью. Нас интересует способ построения оптимального кода, то есть кода, дающего в результате минимальную среднюю длину кодируемого сообщения. Важно отметить, что мы не ищем минимальную длину кода для какого-либо конкретного сообщения или для всех сообщений (последнее найти невозможно), но минимальную длину кода, усредненную по всем возможным сообщениям.
Другой способ взглянуть на данные требования состоит в том, что мы получаем сообщение, уже закодированное путем назначения символам двоичных слов фиксированной длины. Таким образом, если символов 8, каждый символ кодируется тремя битами. Если число символов в алфавите от 9 до 16, то каждый символ кодируется четырьмя битами и т. д. Такое кодирование не является оптимальным, если символы встречаются в сообщениях с разной вероятностью. В этом случае требование может быть сформулировано следующим образом. Требуется разработать оптимальную схему кодирования с использованием кода переменной длины, позволяющую получить кодированное сообщение минимальной средней длины.
Рассмотрим двоичный код с кодовыми длинами L 1 , L 2 …L N , поставленный в соответствие алфавиту из N символов с вероятностями Р 1 , Р 2 ,..., Р N . Для удобства предположим, что символы организованы в порядке убывания вероятности (P 1 >= Р 2 >= ... >= P n ). Можно показать, что оптимальный код должен удовлетворять следующим требованиям:
· Никакие два разных сообщения не должны состоять из одинаковых после
довательностей битов.
· Никакое кодовое слово не должно совпадать с префиксом другого кодового
слова.
· Символы, встречающиеся с большей вероятностью, должны кодироваться более короткими кодовыми словами. То есть L 1 <=L 2 <= ... <=L n .
· Два кодовых слова для символов с наименьшей вероятностью должны иметь
одинаковую длину (L N = L n -1)
и различаться только последней цифрой.
Первое требование гарантирует уникальность кодирования любого сообщения. Второе требование определяет так называемый мгновенный код. Это требование не является строго обязательным, но оно требуется, чтобы гарантировать, что сообщение может быть декодировано шаг за шагом. При продвижении слева направо, как только последовательность битов совпадает с данным кодовым словом, декодирующий алгоритм может произвести соответствующее назначение. Вот пример кода, нарушающего первые два требования:
Двоичная последовательность 010 может соответствовать одному из трех сообщений:
x 2 , x 3 x 1 , x 1 x 4
Назначение третьего требования легко понять, если отметить, что при нарушении данного условия, поменяв два кода, вы сможете получить меньшее значение средней длины. Чтобы понять суть последнего требования, предположим, что L n > L n -1 По второму требованию кодовое слово N - 1 не может быть префиксом кодового слова N. Поэтому первые N- 1 цифры кодового слова N составляют уникальное кодовое слово, а остальные цифры можно отбросить. Если эти два кодовых слова различаются в каком-либо бите, кроме последнего, мы можем отбросить последний бит у каждого слова, получая таким образом лучший код.
На основании этих методов можно построить код, называемый кодом Хаффман. Начнем с упорядочивания всех символов по убыванию вероятности, так что мы получим символы (а 1 , а 2 ,..., a N)
с вероятностями P(a 1) >=Р(а 2) >= ... >=P(а N).
Затем объединим два последних символа в эквивалентный символ с вероятностью Р(а N-1) + Р(а N
).
Коды этих двух символов будут одинаковыми, кроме последних двух цифр. Теперь у нас есть новый набор из N-
1 символов. При необходи
мости поменяем порядок следования символов таким образом, чтобы получить
символы (b 1 , b 2 , ...
b N-1)
с вероятностями P(b 1) >= P(b 2)>= ... >= Р(b N -1).
Теперь мы мо
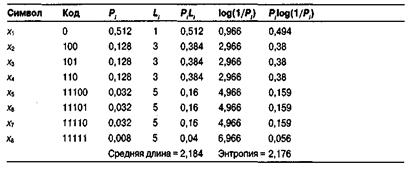
жем повторять этот процесс до тех пор, пока не останется всего два символа. Рисунок ниже иллюстрирует этот процесс для набора символов, заданного в начале раздела. Будем считать каждый символ листовым узлом создаваемого дерева. Объединим два узла с минимальной вероятностью в узел, вероятность которого равна сумме двух соответствующих вероятностей. На каждом шаге будем повторять этот процесс до тех пор, пока не останется только один узел. В результате мы получим дерево, в котором у каждого узла, кроме корневого, одна ветвь отходит направо и две налево. На каждом узле пометим две левые ветви символами 0 и 1 соответственно. Для каждого символа кодовое слово представляет собой строку меток от корневого узла к исходному символу. Все получившиеся в результате кодовые слова показаны в левой части рисунка. Для примера процесс построения кодового слова для символа x 7
обозначен жирной линией.
В таблице ниже приведены свойства кода Хаффмана для данного примера. Средняя длина кодового слова представляет собой вычисляемую следующим образом ожидаемую величину:
![]()
Здесь L i представляет собой длину i-го кодового слова. Таким образом, например, для сообщений, состоящих из 1000 символов, средняя длина кодированного сообщения равна 2184 бит. При простом кодировании каждого символа тремя битами длина этого сообщения будет составлять 3000 бит.
Кодирование Хаффмана является простым алгоритмом для построения кодов переменной длины, имеющих минимальную среднюю длину. Этот весьма популярный алгоритм служит основой многих компьютерных программ сжатия текстовой и графической информации. Некоторые из них используют непосредственно алгоритм Хаффмана, а другие берут его в качестве одной из ступеней многоуровневого процесса сжатия. Метод Хаффмана производит идеальное сжатие (то есть, сжимает данные до их энтропии), если вероятности символов точно равны отрицательным степеням числа 2. Алгоритм начинает строить кодовое дерево снизу вверх, затем скользит вниз по дереву, чтобы построить каждый индивидуальный код справа налево (от самого младшего бита к самому старшему). Начиная с работ Д.Хаффмана 1952 года, этот алгоритм являлся предметом многих исследований. (Последнее утверждение из § 3.8.1 показывает, что наилучший код переменной длины можно иногда получить без этого алгоритма.)
Алгоритм начинается составлением списка символов алфавита в порядке убывания их вероятностей. Затем от корня строится дерево, листьями которого служат эти символы. Это делается по шагам, причем на каждом шаге выбираются два символа с наименьшими вероятностями, добавляются наверх частичного дерева, удаляются из списка и заменяются вспомогательным символом, представляющим эти два символа. Вспомогательному символу приписывается вероятность, равная сумме вероятностей, выбранных на этом шаге символов. Когда список сокращается до одного вспомогательного символа, представляющего весь алфавит, дерево объявляется построенным. Завершается алгоритм спуском по дереву и построением кодов всех символов.
Лучше всего проиллюстрировать этот алгоритм на простом примере. Имеется пять символов с вероятностями, заданными на рис. 1.3а.
Рис. 1.3. Коды Хаффмана.
Символы объединяются в пары в следующем порядке:
1. объединяется с , и оба заменяются комбинированным символом с вероятностью 0.2;
2. Осталось четыре символа, с вероятностью 0.4, а также и с вероятностями по 0.2. Произвольно выбираем и , объединяем их и заменяем вспомогательным символом с вероятностью 0.4;
3. Теперь имеется три символа и с вероятностями 0.4, 0.2 и 0.4, соответственно. Выбираем и объединяем символы и во вспомогательный символ с вероятностью 0.6;
4. Наконец, объединяем два оставшихся символа и и заменяем на с вероятностью 1.
Дерево построено. Оно изображено на рис. 1.3а, «лежа на боку», с корнем справа и пятью листьями слева. Для назначения кодов мы произвольно приписываем бит 1 верхней ветке и бит 0 нижней ветке дерева для каждой пары. В результате получаем следующие коды: 0, 10, 111, 1101 и 1100. Распределение битов по краям - произвольное.
Средняя длина этого кода равна бит/символ. Очень важно то, что кодов Хаффмана бывает много. Некоторые шаги алгоритма выбирались произвольным образом, поскольку было больше символов с минимальной вероятностью. На рис. 1.3b показано, как можно объединить символы по-другому и получить иной код Хаффмана (11, 01, 00, 101 и 100). Средняя длина равна бит/символ как и у предыдущего кода.
Пример: Дано 8 символов А, В, С, D, Е, F, G и H с вероятностями 1/30, 1/30, 1/30, 2/30, 3/30, 5/30, 5/30 и 12/30. На рис. 1.4а,b,с изображены три дерева кодов Хаффмана высоты 5 и 6 для этого алфавита.
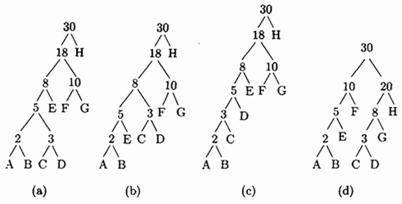
Рис. 1.4. Три дерева Хаффмана для восьми символов.
Средняя длина этих кодов (в битах на символ) равна
Пример : На рис. 1.4d показано другое дерево высоты 4 для восьми символов из предыдущего примера. Следующий анализ показывает, что соответствующий ему код переменной длины плохой, хотя его длина меньше 4.
(Анализ.) После объединения символов А, В, С, D, Е, F и G остаются символы ABEF (с вероятностью 10/30), CDG (с вероятностью 8/30) и H (с вероятностью 12/30). Символы ABEF и CDG имеют наименьшую вероятность, поэтому их необходимо было слить в один, но вместо этого были объединены символы CDG и H. Полученное дерево не является деревом Хаффмана.
Таким образом, некоторый произвол в построении дерева позволяет получать разные коды Хаффмана с одинаковой средней длиной. Напрашивается вопрос: «Какой код Хаффмана, построенный для данного алфавита, является наилучшим?» Ответ будет простым, хотя и неочевидным: лучшим будет код с наименьшей дисперсией.
Дисперсия показывает насколько сильно отклоняются длины индивидуальных кодов от их средней величины (это понятие разъясняется в любом учебнике по статистике). Дисперсия кода 1.3а равна , а для кода 1.3b .
Код 1.3b является более предпочтительным (это будет объяснено ниже). Внимательный взгляд на деревья показывает, как выбрать одно, нужное нам. На дереве рис. 1.3а символ сливается с символом , в то время как на рис. 1.3b он сливается с . Правило будет такое: когда на дереве имеется более двух узлов с наименьшей вероятностью, следует объединять символы с наибольшей и наименьшей вероятностью; это сокращает общую дисперсию кода.
Если кодер просто записывает сжатый файл на диск, то дисперсия кода не имеет значения. Коды Хаффмана с малой дисперсией более предпочтительны только в случае, если кодер будет передавать этот сжатый файл по линиям связи. В этом случае, код с большой дисперсией заставляет кодер генерировать биты с переменной скоростью. Обычно данные передаются по каналам связи с постоянной скоростью, поэтому кодер будет использовать буфер. Биты сжатого файла помещаются в буфер по мере их генерации и подаются в канал с постоянной скоростью для передачи. Легко видеть, что код с нулевой дисперсией будет подаваться в буфер с постоянной скоростью, поэтому понадобится короткий буфер, а большая дисперсия кода потребует использование длинного буфера.
Следующее утверждение можно иногда найти в литературе по сжатию информации: длина кода Хаффмана символа с вероятностью всегда не превосходит . На самом деле, не смотря на справедливость этого утверждения во многих примерах, в общем случае оно не верно. Я весьма признателен Гаю Блелоку, который указал мне на это обстоятельство и сообщил пример кода, приведенного в табл. 1.5. Во второй строке этой таблицы стоит символ с кодом длины 3 бита, в то время как .
Длина кода символа , конечно, зависит от его вероятности . Однако она также неявно зависит от размера алфавита. В большом алфавите вероятности символов малы, поэтому коды Хаффмана имеют большую длину. В маленьком алфавите наблюдается обратная картина. Интуитивно это понятно, поскольку для малого алфавита требуется всего несколько кодов, поэтому все они коротки, а большому алфавиту необходимо много кодов и некоторые из них должны быть длинными.
![]()
Рис. 1.6. Код Хаффмана для английского алфавита.
На рис. 1.6 показан код Хаффмана для всех 26 букв английского алфавита.
Случай алфавита, в котором символы равновероятны, особенно интересен. На рис. 1.7 приведены коды Хаффмана для алфавита с 5, 6, 7 и 8 равновероятными символами. Если размер алфавита является степенью 2, то получаются просто коды фиксированной длины. В других случаях коды весьма близки к кодам с фиксированной длиной. Это означает, что использование кодов переменной длины не дает никаких преимуществ. В табл. 1.8 приведены коды, их средние длины и дисперсии.
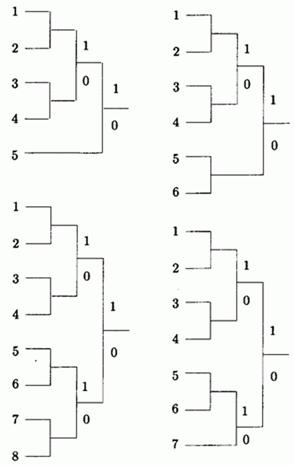
Рис. 1.7. Коды Хаффмана с равными вероятностями.
Тот факт, что данные с равновероятными символами не сжимаются методом Хаффмана может означать, что строки таких символов являются совершенно случайными. Однако, есть примеры строк, в которых все символы равновероятны, но не являются случайными, и их можно сжимать. Хорошим примером является последовательность , в которой каждый символ встречается длинными сериями. Такую строку можно сжать методом RLE, но не методом Хаффмана. (Буквосочетание RLE означает «run-length encoding», т.е. «кодирование длин серий». Этот простой метод сам по себе мало эффективен, но его можно использовать в алгоритмах сжатия со многими этапами, см. ,0);:=Form1.memo1.text;
На рисунке 6 показано, как программа будет выглядеть при открытии файла.
Рисунок 6 - Внешний вид программы при открытии файла
Создание таблицы частот происходит по следующему принципу: символы, встречающиеся в текстовом файле, выписываются в столбец в порядке убывания вероятностей (частоты) их появления. Два последних символа объединяются в один с суммарной вероятностью. Из полученной новой вероятности и вероятностей новых символов, не использованных в объединении, формируется новый столбец в порядке убывания вероятностей, а две последние вновь объединяются. Это продолжается до тех пор, пока не останется одна вероятность, равная сумме вероятностей всех символов, встречающихся в файле.
Листинг тег-кода таблицы частот:
krs:=0;i:=1 to length(s1) do begin:=0;j:=1 to krs dos1[i]=s[j] then:=j;jjj>0 then c:=c+1begin:=krs+1;:=s1[i];:=1;;;.StringGrid1 .colcount:=3;.StringGrid1 .rowcount:=krs+1;i:=1 to krs do begin.stringgrid1.cells :=s[i];.stringgrid1.cells :=inttostr(c[i]);;
При нажатии кнопки Button1Click осуществляется вызов процедуры tablica. В результате чего происходит считывание текстового файла и загрузка его в поле memo1.
Рисунок 7 - Расчет таблицы частот и заполнение поля memo1
При этом в корневой папке программы создается текстовый файл с названием «таблица», в котором отображается рассчитанная таблица частот. В программе это описано следующим образом:
assignfile(f,"таблица.txt");(f);i:=1 to krs do(f,s[i]," ",inttostr(c[i]));
Теперь, когда дерево создано, можно вычислить коды (битовые цепочки для кодирования исходных чисел) и закодировать данные. Опираясь на рисунок 8, нужно уяснить, что вычисление кода числа начинается от корня дерева. Для вычисления кода, необходимо, двигаясь по дереву от корня к числу в исходной таблице, подсчитать число пройденных узлов. Это значение будет равно длине битовой цепочки кода. И проследить для каждого узла повороты, если поворот в узле осуществляется налево, то в цепочке битов устанавливается значение 0, если направо - 1.
Рисунок 8 - Окончательное дерево кодирования Хаффмана
Длительность передачи каждого отдельного кода ti, очевидно, может быть найдена следующим образом: ti = ki , где ki - количество элементарных сигналов (бит) в коде символа i. В соответствии с приведенными выше правилами получаем следующую таблицу кодов:
А01Б100В101Г110Д111Рисунок 9 - Кодировка символов
Рассмотрим описание процедуры кодирования: for i:=1 to krs do begin[i]:=s[i];[i]:=true;[i]:="";;:=krs;n1:=fmin(krs,c,f);:=false;:=fmin(krs,c,f);:=rod;:=rod;i:=1 to krs dorod[i]=r1 then begin[i]:="1"+kod[i];[i]:=r2;rod[i]=r2 then kod[i]:="0"+kod[i];:=c+c;:=kvo-1;kvo=1;i:=1 to length(s1) doj:=1 to krs do begins1[i]=s[j] then s2:=s2+kod[j];; Полученный результат записывается в поле memo2: Form1.memo2.text:=s2; На рисунке 10 показано, что произойдет при нажатии кнопки «Кодировка». Рисунок 10 - Кодировка выражения
При этом в корневой папке программы создается текстовый файл с названием «кодировка», в котором отображается рассчитанная таблица частот. В программе это описано следующим образом: assignfile(ff,"кодировка.txt");(ff); writeln(ff,s2);(ff); Итак, нам удалось сжать выражение, где стоимость хранения входного потока равна 312бит в 87 бит. В дополнении к программе, была создана кнопка «очистить все», которая позволяет очистить таблицу частот, поля memo1 и memo2. Для этого создана кнопка Button3Click. Рассмотрим листинг тег-кода: for i:=0 to Form1.ComponentCount-1 do(Form1.Components[i] is TMemo)then (Form1.Components[i] as TMemo).Clear;(Form1.Components[i] is TEdit)then (Form1.Components[i] as TEdit).Text:="";;k:= 0 to StringGrid1.RowCount - 1 doj:= 0 to StringGrid1.ColCount - 1 do.Cells := ""; Таким образом, при нажатии кнопки «Очистить все» внешний вид программы станет, как при начальном этапе, изображенном на рисунок 5. В итоге, корневая папка будет иметь следующие файлы, показанные на рисунке 11.
Рисунок 11 - Корневая папка
4. Реализация на Delphi метода кодирования Хаффмана
Листинг программы: const nmax=250;masbol= Array of boolean;maschast= Array of integer;: TForm1; {$R *.dfm}s1:string;:string;: array of string;s: array of char;: array of char;: maschast;:byte;tablica;jjj,i,j:integer; var f:textfile;.opendialog1.Filter:="текстовые файлы|*txt|все|*";Form1.openDialog1.Execute and fileexists(Form1.opendialog1.Filename)then.memo1.Lines.LoadFromFile(Form1.openDialog1.FileName) else MessageDlg("что- то не так с файлом",mtwarning,,0); s1:=Form1.memo1.text;:=0;i:=1 to length(s1) do begin:=0;j:=1 to krs dos1[i]=s[j] then:=j;jjj>0 then c:=c+1begin:=krs+1;:=s1[i];:=1;;;.StringGrid1 .colcount:=3;.StringGrid1 .rowcount:=krs+1;i:=1 to krs do begin.stringgrid1.cells :=s[i];.stringgrid1.cells :=inttostr(c[i]);;(f,"таблица.txt");(f);i:=1 to krs do(f,s[i]," ",inttostr(c[i]));(f);;TForm1.Button1Click(Sender: TObject);;;fmin(k:integer;v:maschast;f:masbol):integer;imin,min,i:integer;:=32767;:=0;i:=1 to k dof[i] and (min>v[i]) then begin:=v[i];:=i;;:=imin;;TForm1.Button2Click(Sender: TObject);n1,n2,i,j,kvo:integer;,r2:char;:masbol;:textfile;i:=1 to krs do begin[i]:=s[i];[i]:=true;[i]:="";;:=krs;n1:=fmin(krs,c,f);:=false;:=fmin(krs,c,f);:=rod;:=rod;i:=1 to krs dorod[i]=r1 then begin[i]:="1"+kod[i];[i]:=r2;rod[i]=r2 then[i]:="0"+kod[i];:=c+c;:=kvo-1;kvo=1;i:=1 to length(s1) doj:=1 to krs do begins1[i]=s[j] then:=s2+kod[j];;.memo2.text:=s2;(ff,"кодировка.txt");(ff);(ff,s2);(ff);;TForm1.Button3Click(Sender: TObject);i,k,j:integer;i:=0 to Form1.ComponentCount-1 do(Form1.Components[i] is TMemo)then (Form1.Components[i] as TMemo).Clear;(Form1.Components[i] is TEdit)then (Form1.Components[i] as TEdit).Text:="";;k:= 0 to StringGrid1.RowCount - 1 doj:= 0 to StringGrid1.ColCount - 1 do.Cells := ""; Заключение
В данной курсовой работе была поставлена задача разработать программу для классического метода кодирования Хаффмана на Delphi версии 7.0. Первым такой алгоритм опубликовал Дэвид Хаффман (David Huffman) в 1952 году. Алгоритм Хаффмана двухпроходный. На первом проходе строится частотный словарь и генерируются коды. На втором проходе происходит непосредственно кодирование. Стоит отметить, что за 50 лет со дня опубликования, код Хаффмана ничуть не потерял своей актуальности и значимости. Так с уверенностью можно сказать, что мы сталкиваемся с ним, в той или иной форме (дело в том, что код Хаффмана редко используется отдельно, чаще работая в связке с другими алгоритмами), практически каждый раз, когда архивируем файлы, смотрим фотографии, фильмы, посылаем факс или слушаем музыку. Кодирование Хаффмана является простым алгоритмом для построения кодов переменной длины, имеющих минимальную среднюю длину. Этот весьма популярный алгоритм служит основой многих компьютерных программ сжатия текстовой и графической информации. Некоторые из них используют непосредственно алгоритм Хаффмана, а другие берут его в качестве одной из ступеней многоуровневого процесса сжатия. Суть данного алгоритма заключается в построении двоичного дерева с узловыми элементами из символов входного алфавита. И чем больше вероятность появления символа в тексте, тем ближе он к корню. Каждой ветви назначается «вес» - битовый ноль или единица. Кодирование каждого символа осуществляется проходом по дереву и выбором одной из двух ветвей, начиная с корня дерева и заканчивая листом с нужным символом. Метод Хаффмана широко используется, но постепенно вытесняется арифметическим сжатием. Свою роль в этом сыграло то, что закончились сроки действия патентов, ограничивающих использование арифметического сжатия. Кроме того, алгоритм Хаффмана не является оптимальным. Он приближает относительные частоты появления символа в потоке частотами, представляющими собой отрицательные степени двойки, в то время как арифметическое сжатие дает лучшую степень приближения частоты.
Сжатие информации в ПК
1. Основные понятия и методы сжатия данных. Во многих стадиях информация, содержащаяся в файлах, избыточна.
...арифметическим кодированием, имеющим схожую с кодом Хаффмана функцию и основанным на идее кодирования символов дробным числом битов.
- code = следующий бит из потока, length = 1
- Пока code < base
code = code << 1
code = code + следующий бит из потока
length = length + 1 - symbol = symb + code - base]
Другими словами, будем вдвигать слева в переменную code бит за битом из входного потока, до тех пор, пока code < base. При этом на каждой итерации будем увеличивать переменную length на 1 (т.е. продвигаться вниз по дереву). Цикл в (2) остановится когда мы определим длину кода (уровень в дереве, на котором находится искомый символ). Остается лишь определить какой именно символ на этом уровне нам нужен.
Предположим, что цикл в (2), после нескольких итераций, остановился. В этом случае выражение (code - base) суть порядковый номер искомого узла (символа) на уровне length. Первый узел (символ), находящийся на уровне length в дереве, расположен в массиве symb по индексу offs. Но нас интересует не первый символ, а символ под номером (code - base). Поэтому индекс искомого символа в массиве symb равен (offs + (code - base)). Иначе говоря, искомый символ symbol=symb + code - base].
Приведем конкретный пример. Пользуясь изложенным алгоритмом декодируем сообщение Z / .
Z / ="0001 1 00001 00000 1 010 011 1 011 1 010 011 0001 1 0010 010 011 011 1 1 1 010 1 1 1 0010 011 0011 1 0011 0011 011 1 010 1 1"
- code = 0, length = 1
- code = 0 < base = 1
code = 0 << 1 = 0
code = 0 + 0 = 0
length = 1 + 1 = 2
code = 0 < base = 2
code = 0 << 1 = 0
code = 0 + 0 = 0
length = 2 + 1 = 3
code = 0 < base = 2
code = 0 << 1 = 0
code = 0 + 1 = 1
length = 3 + 1 = 4
code = 1 = base = 1 - symbol = symb = 2 + code = 1 - base = 1] = symb = A
- code = 1, length = 1
- code = 1 = base = 1
- symbol = symb = 7 + code = 1 - base = 1] = symb = H
- code = 0, length = 1
- code = 0 < base = 1
code = 0 << 1 = 0
code = 0 + 0 = 0
length = 1 + 1 = 2
code = 0 < base = 2
code = 0 << 1 = 0
code = 0 + 0 = 0
length = 2 + 1 = 3
code = 0 < base = 2
code = 0 << 1 = 0
code = 0 + 0 = 0
length = 3 + 1 = 4
code = 0 < base = 1
code = 0 << 1 = 0
code = 0 + 1 = 1
length = 4 + 1 = 5
code = 1 > base = 0 - symbol = symb = 0 + code = 1 - base = 0] = symb = F
Итак, мы декодировали 3 первых символа: A , H , F . Ясно, что следуя этому алгоритму мы получим в точности сообщение S.
Вычисление длин кодов
Для того чтобы закодировать сообщение нам необходимо знать коды символов и их длины. Как уже было отмечено в предыдущем разделе, канонические коды вполне определяются своими длинами. Таким образом, наша главная задача заключается в вычислении длин кодов.
Оказывается, что эта задача, в подавляющем большинстве случаев, не требует построения дерева Хаффмана в явном виде. Более того, алгоритмы использующие внутреннее (не явное) представление дерева Хаффмана оказываются гораздо эффективнее в отношении скорости работы и затрат памяти.
На сегодняшний день существует множество эффективных алгоритмов вычисления длин кодов ( , ). Мы ограничимся рассмотрением лишь одного из них. Этот алгоритм достаточно прост, но несмотря на это очень популярен. Он используется в таких программах как zip, gzip, pkzip, bzip2 и многих других.
Вернемся к алгоритму построения дерева Хаффмана. На каждой итерации мы производили линейный поиск двух узлов с наименьшим весом. Ясно, что для этой цели больше подходит очередь приоритетов, такая как пирамида (минимальная). Узел с наименьшим весом при этом будет иметь наивысший приоритет и находиться на вершине пирамиды. Приведем этот алгоритм.
Включим все кодируемые символы в пирамиду.
Последовательно извлечем из пирамиды 2 узла (это будут два узла с наименьшим весом).
Сформируем новый узел и присоединим к нему, в качестве дочерних, два узла взятых из пирамиды. При этом вес сформированного узла положим равным сумме весов дочерних узлов.
Включим сформированный узел в пирамиду.
Если в пирамиде больше одного узла, то повторить 2-5.
Будем считать, что для каждого узла сохранен указатель на его родителя. У корня дерева этот указатель положим равным NULL. Выберем теперь листовой узел (символ) и следуя сохраненным указателям будем подниматься вверх по дереву до тех пор, пока очередной указатель не станет равен NULL. Последнее условие означает, что мы добрались до корня дерева. Ясно, что число переходов с уровня на уровень равно глубине листового узла (символа), а следовательно и длине его кода. Обойдя таким образом все узлы (символы), мы получим длины их кодов.
Максимальная длина кода
Как правило, при кодировании используется так называемая кодовая книга (CodeBook) , простая структура данных, по сути два массива: один с длинами, другой с кодами. Другими словами, код (как битовая строка) хранится в ячейке памяти или регистре фиксированного размера (чаще 16, 32 или 64). Для того чтобы не произошло переполнение, мы должны быть уверены в том, что код поместится в регистр.
Оказывается, что на N-символьном алфавите максимальный размер кода может достигать (N-1) бит в длину. Иначе говоря, при N=256 (распространенный вариант) мы можем получить код в 255 бит длиной (правда для этого файл должен быть очень велик: 2.292654130570773*10^53~=2^177.259)! Ясно, что такой код в регистр не поместится и с ним нужно что-то делать.
Для начала выясним при каких условиях возникает переполнение. Пусть частота i-го символа равна i-му числу Фибоначчи. Например: A -1, B -1, C -2, D -3, E -5, F -8, G -13, H -21. Построим соответствующее дерево Хаффмана.
ROOT /\ / \ / \ /\ H / \ / \ /\ G / \ / \ /\ F / \ / \ /\ E / \ / \ /\ D / \ / \ /\ C / \ / \ A B
Такое дерево называется вырожденным . Для того чтобы его получить частоты символов должны расти как минимум как числа Фибоначчи или еще быстрее. Хотя на практике, на реальных данных, такое дерево получить практически невозможно, его очень легко сгенерировать искусственно. В любом случае эту опасность нужно учитывать.
Эту проблему можно решить двумя приемлемыми способами. Первый из них опирается на одно из свойств канонических кодов. Дело в том, что в каноническом коде (битовой строке) не более младших бит могут быть ненулями. Другими словами, все остальные биты можно вообще не сохранять, т.к. они всегда равны нулю. В случае N=256 нам достаточно от каждого кода сохранять лишь младшие 8 битов, подразумевая все остальные биты равными нулю. Это решает проблему, но лишь отчасти. Это значительно усложнит и замедлит как кодирование, так и декодирование. Поэтому этот способ редко применяется на практике.
Второй способ заключается в искусственном ограничении длин кодов (либо во время построения, либо после). Этот способ является общепринятым, поэтому мы остановимся на нем более подробно.
Существует два типа алгоритмов ограничивающих длины кодов. Эвристические (приблизительные) и оптимальные. Алгоритмы второго типа достаточно сложны в реализации и как правило требуют больших затрат времени и памяти, чем первые. Эффективность эвристически-ограниченного кода определяется его отклонением от оптимально-ограниченного. Чем меньше эта разница, тем лучше. Стоит отметить, что для некоторых эвристических алгоритмов эта разница очень мала ( , , ), к тому же они очень часто генерируют оптимальный код (хотя и не гарантируют, что так будет всегда). Более того, т.к. на практике переполнение случается крайне редко (если только не поставлено очень жесткое ограничение на максимальную длину кода), при небольшом размере алфавита целесообразнее применять простые и быстрые эвристические методы.
Мы рассмотрим один достаточно простой и очень популярный эвристический алгоритм. Он нашел свое применение в таких программах как zip, gzip, pkzip, bzip2 и многих других.
Задача ограничения максимальной длины кода эквивалентна задаче ограничения высоты дерева Хаффмана. Заметим, что по построению любой нелистовой узел дерева Хаффмана имеет ровно два потомка. На каждой итерации нашего алгоритма будем уменьшать высоту дерева на 1. Итак, пусть L - максимальная длина кода (высота дерева) и требуется ограничить ее до L / < L. Пусть далее RN i самый правый листовой узел на уровне i, а LN i - самый левый.
Начнем работу с уровня L. Переместим узел RN L на место своего родителя. Т.к. узлы идут парами нам необходимо найти место и для соседного с RN L узла. Для этого найдем ближайший к L уровень j, содержащий листовые узлы, такой, что j < (L-1). На месте LN j сформируем нелистовой узел и присоединим к нему в качестве дочерних узел LN j и оставшийся без пары узел с уровня L. Ко всем оставшимся парам узлов на уровне L применим такую же операцию. Ясно, что перераспределив таким образом узлы, мы уменьшили высоту нашего дерева на 1. Теперь она равна (L-1). Если теперь L / < (L-1), то проделаем то же самое с уровнем (L-1) и т.д. до тех пор, пока требуемое ограничение не будет достигнуто.
D G B CТаким образом, мы ограничили максимальную длину кода до 4. Ясно, что изменив длины кодов, мы немного потеряли в эффективности. Так сообщение S, закодированное при помощи такого кода, будет иметь размер 92 бита, т.е. на 3 бита больше по сравнению с минимально-избыточным кодом.
Ясно, что чем сильнее мы ограничим максимальную длину кода, тем менее эффективен будет код. Выясним насколько можно ограничивать максимальную длину кода. Очевидно что не короче бит.
Вычисление канонических кодов
Как мы уже неоднократно отмечали, длин кодов достаточно для того чтобы сгенерировать сами коды. Покажем как это можно сделать. Предположим, что мы уже вычислили длины кодов и подсчитали сколько кодов каждой длины у нас есть. Пусть L - максимальная длина кода, а T i - количество кодов длины i.
Вычислим S i - начальное значение кода длины i, для всех i из
S L = 0 (всегда)
S L-1 = (S L + T L) >> 1
S L-2 = (S L-1 + T L-1) >> 1
...
S 1 = 1 (всегда)
Для нашего примера L = 5, T 1 .. 5 = {1, 0, 2 ,3, 2}.
S 5 = 00000 bin = 0 dec
S 4 = (S 5 =0 + T 5 =2) >> 1 =
(00010 bin >> 1) = 0001 bin = 1 dec
S 3 = (S 4 =1 + T 4 =3) >> 1 =
(0100 bin >> 1) = 010 bin = 2 dec
S 2 = (S 3 =2 + T 3 =2) >> 1 =
(100 bin >> 1) = 10 bin = 2 dec
S 1 = (S 2 =2 + T 2 =0) >> 1 =
(10 bin >> 1) = 1 bin = 1 dec
Видно, что S 5 , S 4 , S 3 , S 1 - в точности коды символов B , A , C , H . Эти символы объединяет то, что все они стоят на первом месте, каждый на своем уровне. Другими словами, мы нашли начальное значение кода для каждой длины (или уровня).
Теперь присвоим коды остальным символам. Код первого символа на уровне i равен S i , второго S i + 1, третьего S i + 2 и т.д.
Выпишем оставшиеся коды для нашего примера:
| B = S 5 = 00000 bin | A = S 4 = 0001 bin | C = S 3 = 010 bin | H = S 1 = 1 bin |
| F = S 5 + 1 = 00001 bin | D = S 4 + 1 = 0010 bin | E = S 3 + 1 = 011 bin | |
| G = S 4 + 2 = 0011 bin |
Видно, что мы получили точно такие же коды, как если бы мы явно построили каноническое дерево Хаффмана.
Передача кодового дерева
Для того чтобы закодированное сообщение удалось декодировать, декодеру необходимо иметь такое же кодовое дерево (в той или иной форме), какое использовалось при кодировании. Поэтому вместе с закодированными данными мы вынуждены сохранять соответствующее кодовое дерево. Ясно, что чем компактнее оно будет, тем лучше.
Решить эту задачу можно несколькими способами. Самое очевидное решение - сохранить дерево в явном виде (т.е. как упорядоченное множество узлов и указателей того или иного вида). Это пожалуй самый расточительный и неэффективный способ. На практике он не используется.
Можно сохранить список частот символов (т.е. частотный словарь). С его помощью декодер без труда сможет реконструировать кодовое дерево. Хотя этот способ и менее расточителен чем предыдущий, он не является наилучшим.
Наконец, можно использовать одно из свойств канонических кодов. Как уже было отмечено ранее, канонические коды вполне определяются своими длинами. Другими словами, все что необходимо декодеру - это список длин кодов символов. Учитывая, что в среднем длину одного кода для N-символьного алфавита можно закодировать [(log 2 (log 2 N))] битами, получим очень эффективный алгоритм. На нем мы остановимся подробнее.
Предположим, что размер алфавита N=256, и мы сжимаем обыкновенный текстовый файл (ASCII). Скорее всего мы не встретим все N символов нашего алфавита в таком файле. Положим тогда длину кода отсутвующих символов равной нулю. В этом случае сохраняемый список длин кодов будет содержать достаточно большое число нулей (длин кодов отсутствующих символов) сгруппированных вместе. Каждую такую группу можно сжать при помощи так называемого группового кодирования - RLE (Run - Length - Encoding). Этот алгоритм чрезвычайно прост. Вместо последовательности из M одинаковых элементов идущих подряд, будем сохранять первый элемент этой последовательности и число его повторений, т.е. (M-1). Пример: RLE("AAAABBBCDDDDDDD")=A3 B2 C0 D6.
Более того, этот метод можно несколько расширить. Мы можем применить алгоритм RLE не только к группам нулевых длин, но и ко всем остальным. Такой способ передачи кодового дерева является общепринятым и применяется в большинстве современных реализаций.
Реализация: SHCODEC
Приложение: биография Д. Хаффмана
Дэвид Хаффман родился в 1925 году в штате Огайо (Ohio), США. Хаффман получил степень бакалавра электротехники в государственном университете Огайо (Ohio State University) в возрасте 18 лет. Затем он служил в армии офицером поддержки радара на эсминце, который помогал обезвреживать мины в японских и китайских водах после Второй Мировой Войны. В последствии он получил степень магистра в университете Огайо и степень доктора в Массачусетском Институте Технологий (Massachusetts Institute of Technology - MIT). Хотя Хаффман больше известен за разработку метода построения минимально-избыточных кодов, он так же сделал важный вклад во множество других областей (по большей части в электронике). Он долгое время возглавлял кафедру Компьютерных Наук в MIT. В 1974, будучи уже заслуженным профессором, он подал в отставку. Хаффман получил ряд ценных наград. В 1999 - Медаль Ричарда Хамминга (Richard W. Hamming Medal) от Института Инженеров Электричества и Электроники (Institute of Electrical and Electronics Engineers - IEEE) за исключительный вклад в Теорию Информации, Медаль Louis E. Levy от Франклинского Института (Franklin Institute) за его докторскую диссертацию о последовательно переключающихся схемах, Награду W. Wallace McDowell, Награду от Компьютерного Сообщества IEEE, Золотую юбилейную награду за технологические новшества от IEEE в 1998. В октябре 1999 года, в возрасте 74 лет Дэвид Хаффман скончался от рака. |






